什么是柏拉图立体? 在我们所能直观感知的三维世界中,最为和谐规则的多面体模过于柏拉图立体何为柏拉图立体呢,啰嗦一点来说满足以下条件的立体图形就是柏拉图立体:1.所有的面都是正多边形;2.所有的面大小和形状都相同;
3.每一个角上有相同数量的面 想来也就是除了球以外最最中规中矩的立体图形:每一个顶点,每一条棱,每一个面都具有同等的地位 这样完美的图形当然是非常稀有的,前人已经证明了柏拉图立体只有5个,它们分别是正四面体(由4个等边三角形组成)、正六面体(由6个正方形组成)、正八面体(由8个等边三角形组成)、正十二面体(由12个正五边形组成)、正二十面体(由20个等边三角形组成)。
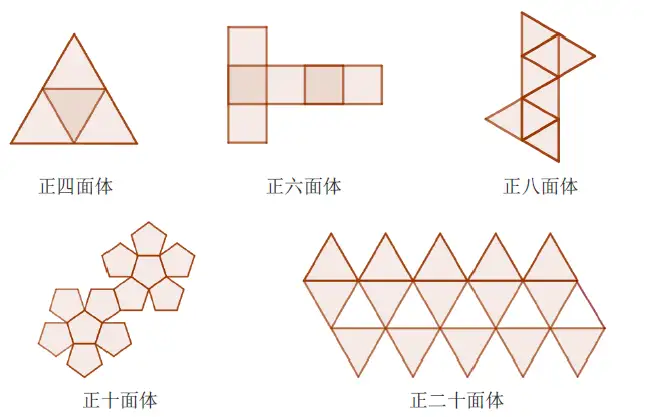
【平面展开图】
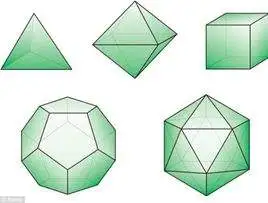
立体直观图(来自度娘)如何证明柏拉图立体只有5种?法①:穷举法 拿正多边形来拼顶角,容易知道,要形成立体图形每个点至少要有3个面.1.每个面都是正三角形,用3个三角形,得到正四面体 4个三角形,得到正八面体
5个三角形,得到正二十面体 6个三角形,6×60°=360°,不满足 6个以上,更加不满足2.每个面都是正方形,用3个正方形,得到正六面体 4个正方形,4×90°=360°,不满足
4个以上,更加不满足3.每个面都是五边形,用3个五边形,得到正十二面体 4个五边形,4×108°>360°,不满足 4个以上不满足4.每个面都是六边形,用3个六边形,3×120°=360°,不满足
所以以后的情况都不满足.法② 设正多面体每个顶点处有m(m≥3)个面组成,则每个面对应的夹角要小于2π/m,而每个面均为正多边形,正n边形每个内角大小为((n-2)π)/n,得到不等式((n-2)π)/n<2π/m.
解得(n,m)只能为(3,3)、(3,4)、(3,5)、(4,3)、(5,3),分别对应正四面体、正六面体、正十二面体、正八面体、正二十面体法③ 利用欧拉定理 设每个顶点连接m(m≥3)个正n(n≥3)边形,由欧拉定理,v+f-e=2,其中v为顶点数,f为面数,e为棱数.。
正多面体每个顶点连接相同数量的棱,即e=mv/2.每个面都是n边形,有e=nf/2.线性规划得出m,n只有5组正整数解.

 sdf
sdf